Technique
- Let us say we have a book of "600" pages and we want to read page number "338", one method is to apply linear search and turn pages one by one which is very time consuming and inefficient.
- Another way is that we can randomly open a page from book which may be near to 338, suppose we opened page number 420. Now we will only search our page in the left part of the book i.e. between 1 to 420.
- Again say we got to page number 330 so, now we will search between page 330 to 420.
- This way we can reach our page in a much efficient way.
- Binary Search will work in a similar manner, which can only be applied on sorted data.
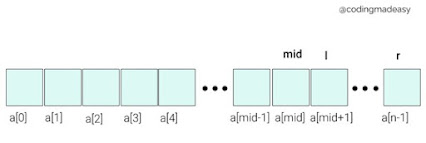
- In this method we will compare the item to be searched with the item at middle index of array.
- Say "l" is lower bound & "r" is upper bound of array, so middle will be calculated as mid = ( l + r ) / 2.
- Then we will compare our item with "a[mid]" element of our Array as follows:
if ( item == a[mid] )
return mid;
else if ( item > a[mid] )
l = mid + 1;
else
r = mid - 1;
- If item == a[mid] i.e. item is found then, we will return "mid" and our search is successful.
- If item > a[mid] i.e. "item" is greater than "a[mid]" then we set "l" to the element on the right of "mid" & "r" remains at its position.
- It means item exist between "mid + 1" & "r".
- Now, we will again calculate "mid" & repeat the process.
- If item < a[mid] i.e. "item" is less than "a[mid]" then we set "r" to the element on the left of "mid". "l" remains at its position.
- It means item exist between "l" & "mid - 1".
- We will stop our search when "l" becomes greater than "r". It means search is unsuccessful and we will return -1.
Program
Example
- We will take three variables "l" , "r", & "mid". Initially we will take l=0 & r=6. (Lower Bound=0 & Upper Bound=6)
- Then we will calculate index of middle element of our Array as ( l + r ) / 2 and store the result in mid.
mid=( l + r ) / 2 = ( 0 + 6 ) / 2 = 3. - Now we will compare our item "17" with a[mid] i.e. a[3], Both are not equal.
- So, we will check whether our item "17" is greater than a[3] or not. As "17" is greater than "10". So, "17" might exist between "mid + 1" & "r".
- It will reduce our search bracket. Now we will set "l = mid + 1" & r will remain unchanged, i.e. "l = 4" & "r = 6".
- Now again we will calculate mid = ( l + r )/2 = ( 4 + 6 )/2 = 5.
- Now we will compare our item "17" with a[mid] i.e. a[5], Both are equal and our search is successful so, our algorithm will return "mid" i.e. "5".
Let us take another example
- Suppose we want to find location of item "2" in Array given below:
- Again we will set l=0 & r=6. (Lower Bound=0 & Upper Bound=6)
- Set mid = ( l + r ) / 2 = ( 0 + 6 ) / 2 = 3.
- Now we will compare our item "2" with a[mid] i.e. a[3], Both are not equal.
- So, we will check whether our item "2" is greater than a[3] or not. As "2" is not greater than "10". So, "2" is less than a[mid] and "2" might exist between "l" & "mid-1".
- It will reduce our search bracket. Now we will set "r = mid - 1" & "l" will remain unchanged, i.e. "l = 0" & "r = 2".
- Now again we will calculate mid=( l + r )/2 = ( 0 + 2 )/2 = 1.
- We will compare our item "2" with a[mid] i.e. a[1]. Again both are not equal.
- So, we will check whether our item "2" is greater than a[1] or not. Again "2" is not greater than "5". It means "2" is less than a[mid] and "2" might exist between "l" & "mid-1".
- It will reduce our search bracket. Now we will set "r = mid - 1" & "l" will remain unchanged, i.e. "l = 0" & "r = 0".
- We will calculate mid = ( l + r ) / 2 = ( 0 + 0 ) / 2 = 0.

Binary Search Complexity
- In Best case Binary Search will find the location of item in
given array in only 1 comparison so, it is O(1).
.
- In Worst case at each iteration of Binary Search the array size will be reduced to its half.
- At iteration 1, size of array = n
- At iteration 2, size of array = n/2
- At iteration 3, size of array = n/4
- At iteration k, size of array = 1 .i.e. n/2^k = 1 => n = 2^k => k=log(n)
- So, in Worst Case Complexity of Binary Search is O(log(n).
- In Average case of Binary Search item could be found in:
1 comparison or 2 comparisons or 3 comparisons.. or log(n) comparisons where log(n) = m.
- So, Total comparisons (1+2+3+..+m)
- Total no. of cases = m
- Average Comparisons = (1+2+3+...+m)/m where m = log(n).
= m ( m + 1 ) / 2m
= ( m + 1 ) / 2
= ( log(n) + 1 ) / 2
.
- So, Average Complexity of Binary Search is O(log(n)).
- In Best case Binary Search will find the location of item in given array in only 1 comparison so, it is O(1). .
- In Worst case at each iteration of Binary Search the array size will be reduced to its half.
- At iteration 1, size of array = n
- At iteration 2, size of array = n/2
- At iteration 3, size of array = n/4
- At iteration k, size of array = 1 .i.e. n/2^k = 1 => n = 2^k => k=log(n)
- So, in Worst Case Complexity of Binary Search is O(log(n).
- In Average case of Binary Search item could be found in: 1 comparison or 2 comparisons or 3 comparisons.. or log(n) comparisons where log(n) = m.
- So, Total comparisons (1+2+3+..+m)
- Total no. of cases = m
- Average Comparisons = (1+2+3+...+m)/m where m = log(n).
= m ( m + 1 ) / 2m
= ( m + 1 ) / 2
= ( log(n) + 1 ) / 2
.
- So, Average Complexity of Binary Search is O(log(n)).













No comments:
Post a Comment