UGC-NET Computer Science Data Structures Questions with Explanation

In this Blog we are providing all the UGC-NET Computer Science previous year Questions with explanation:

Q::7 Number of binary trees formed with 5
nodes are
(A) 32 (B) 36
(C) 120 (D) 42

Answer:(D)

Explanation:

In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involving recursively-defined objects. They are named after the Belgian mathematician Eugène Charles Catalan (1814–1894).

Using zero-based numbering, the nth Catalan number is given directly in terms of binomial coefficients by

The first Catalan numbers for n = 0, 1, 2, 3, … are

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, … 

Applications in combinatorics

There are many counting problems in combinatorics whose solution is given by the Catalan numbers. The book Enumerative Combinatorics: Volume 2 by combinatorialist Richard P. Stanley contains a set of exercises which describe 66 different interpretations of the Catalan numbers. Following are some examples, with illustrations of the cases C₃ = 5 and C₄ = 14.

Lattice of the 14 Dyck words of length 8 - ( and ) interpreted as up anddown

• C_n is the number of Dyck words of length 2n. A Dyck word is a string consisting of n X's and n Y's such that no initial segment of the string has more Y's than X's (see also Dyck language). For example, the following are the Dyck words of length 6:

XXXYYY     XYXXYY     XYXYXY     XXYYXY     XXYXYY.

• Re-interpreting the symbol X as an open parenthesis and Y as a close parenthesis, C_n counts the number of expressions containing n-pairs of parentheses which are correctly matched:

((()))     ()(())     ()()()     (())()     (()())

• C_n is the number of different ways n + 1 factors can be completely parenthesized (or the number of ways of associating n applications of a binary operator). For n = 3, for example, we have the following five different parenthesizations of four factors:

((ab)c)d     (a(bc))d     (ab)(cd)     a((bc)d)     a(b(cd))

The associahedron of order 4 with the C₄=14 full binary trees with 5 leaves

• Successive applications of a binary operator can be represented in terms of a full binary tree. (A rooted binary tree is full if every vertex has either two children or no children.) It follows that C_n is the number of full binary trees with n + 1 leaves:

• C_n is the number of non-isomorphic ordered trees with n vertices. (An ordered tree is a rooted tree in which the children of each vertex are given a fixed left-to-right order.)
• C_n is the number of monotonic lattice paths along the edges of a grid with n × n square cells, which do not pass above the diagonal. A monotonic path is one which starts in the lower left corner, finishes in the upper right corner, and consists entirely of edges pointing rightwards or upwards. Counting such paths is equivalent to counting Dyck words: X stands for "move right" and Y stands for "move up".

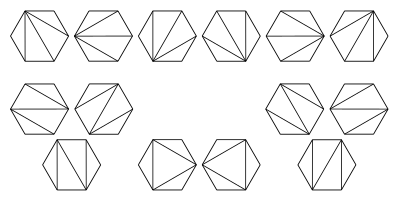
The following diagrams show the case n = 4:

This can be succinctly represented by listing the Catalan elements by column height:

[0,0,0,0][0,0,0,1][0,0,0,2][0,0,1,1]

[0,1,1,1] [0,0,1,2] [0,0,0,3] [0,1,1,2][0,0,2,2][0,0,1,3]

[0,0,2,3][0,1,1,3] [0,1,2,2][0,1,2,3]

The triangles correspond to nodes of the binary trees.

• C_n is the number of different ways a convex polygon with n + 2 sides can be cut into triangles by connecting vertices with straight lines(a form of Polygon triangulation). The following hexagons illustrate the case n = 4:

• C_n is the number of stack-sortable permutations of {1, ..., n}. A permutation w is called stack-sortable if S(w) = (1, ..., n), where S(w) is defined recursively as follows: write w = unv where n is the largest element in w and u and v are shorter sequences, and set S(w) = S(u)S(v)n, with S being the identity for one-element sequences. These are the permutations that avoid the pattern 231.
• C_n is the number of permutations of {1, ..., n} that avoid the pattern 123 (or any of the other patterns of length 3); that is, the number of permutations with no three-term increasing sub-sequence. For n = 3, these permutations are 132, 213, 231, 312 and 321. For n = 4, they are 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312 and 4321.
• C_n is the number of non-crossing partitions of the set {1, ..., n}. A fortiori, C_n never exceeds the nth Bell number. C_n is also the number of non-crossing partitions of the set {1, ..., 2n} in which every block is of size 2. The conjunction of these two facts may be used in a proof by mathematical induction that all of the free cumulants of degree more than 2 of the Wigner semicircle law are zero. This law is important in free probability theory and the theory of random matrices.
• C_n is the number of ways to tile a stairstep shape of height n with n rectangles. The following figure illustrates the case n = 4:

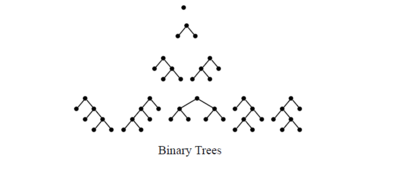
• C_n is the number of rooted binary trees with n internal nodes (n + 1 leaves or external nodes). Illustrated in following Figure are the trees corresponding to n = 0,1,2 and 3. There are 1, 1, 2, and 5 respectively. Here, we consider as binary trees those in which each node has zero or two children, and the internal nodes are those that have children.